Y=x^2 2 parabola 572665-Graph parabola y=(x+2)^2+5
Step 1 Solve for the vertex of the parabola The vertex of a parabola of the form {eq}y= x^2 bx c {/eq} is always given by {eq}\left (\dfrac {b} {2a},f (\dfrac {b} {2a})\right) {/eq} StepParabola Calculator This calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose theKey Takeaways The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola;

Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
Graph parabola y=(x+2)^2+5
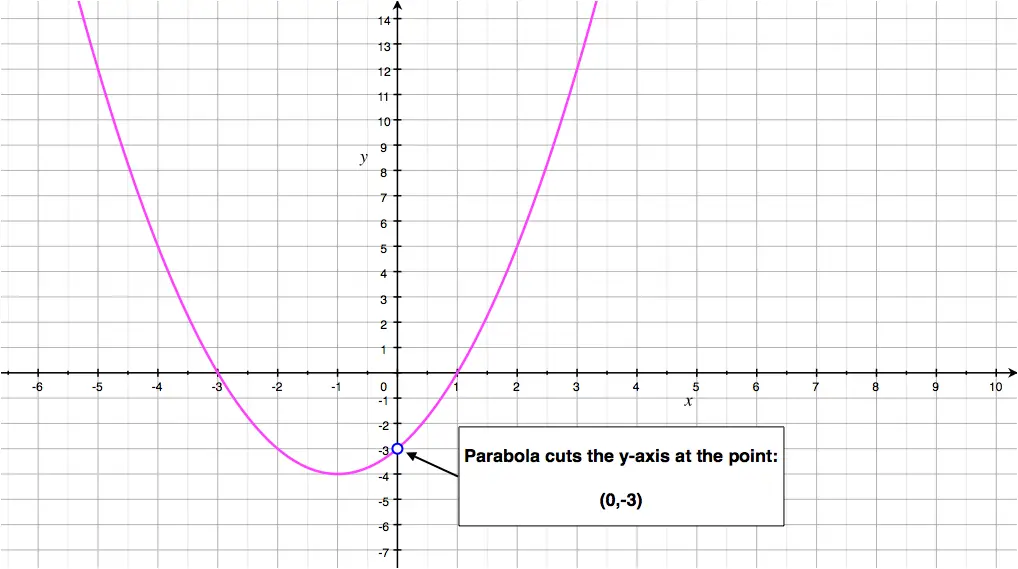
Graph parabola y=(x+2)^2+5-The parabola defined by \y = x^22x3\ has \(y\)intercept at \\begin{pmatrix}0,3\end{pmatrix}\ Where \(3\) is the only term without an \(x\) in the parabola's equation This can be seen on this parabola's graph We can see that \(y=x^22x3\) cuts the \(y\)axis at the point \(\begin{pmatrix}0,3 \end{pmatrix}\)For each of the following parabolas, find its xintercept(s), yintercept and vertex (a) y = x 2 4 x − 12 (b) y = − x 2 6 x − 7 (c) y = 2 x 2 2 x 7 010 Systems of Equations A system of two equations in two unknowns x and y can be written as F 1 (x, y) = 0 F 2 (x, y) = 0 Usually, each equation represents a curve in the




Content Transformations Of The Parabola
Exploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the thirdIn this video we're going to talk about one of the most common types of curves you will see in mathematics and that is the parabola and the word parabola sounds quite fancy but we'll see it's describing something that is fairly straightforward now in terms of why it is called the parabola I've seen multiple explanations for it it comes from Greek para that root word similar to parable youSwitch nargin case 0 pparse() case 1 pparse(a) case 2 pparse(a, b) But as someone pointed out below, this doesn't replicate the behavior in my initial code block where it uses the default value if the input is empty I think given that, I'll just stick with a template Thanks again for the help!
The vertex form of the equation of a parabola is y=(x3)^236 what is the standard form of the equation rosieweber04 rosieweber04 Mathematics High School answered The vertex form of the equation of a parabola is y=(x3)^236 what is the standard form of the equation 2 See answers 2 Rotating the parabola y = x2 by θ clockwise gives v = u2, where (u v) = (cosθ − sinθ sinθ cosθ)(x y) ie xsinθ ycosθ = (xcosθ − ysinθ)2 Putting θ = π 4 gives 1 √2(x y) = ( 1 √2(x − y))2√2(x y) = (x − y)2 which when expanded is x2Sideways Parabolas 1 Cool Math has free online cool math lessons, cool math games and fun math activities Really clear math lessons (prealgebra, algebra, precalculus), cool math games, online graphing calculators, geometry art, fractals, polyhedra, parents and teachers areas too
But avoid Asking for help, clarification, or responding to other answers Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open down We actually have 2 functions, y = √ x (the top half of the parabola);



Graphing Quadratic Functions




Parabola Parent Function Mathbitsnotebook A1 Ccss Math
Matemáticas Funciones básicas Estudio y representación de parábolas y=x^2 y=ax^2bxc Estudio de las funciones polinómicas de segundo grado RepresentaFree Parabola Vertex calculator Calculate parabola vertex given equation stepbystep This website uses cookies to ensure you get the best experienceThe simplest equation of a parabola is y 2 = x when the directrix is parallel to the yaxis In general, if the directrix is parallel to the yaxis in the standard equation of a parabola is given as y2 = 4ax If the parabola is sideways ie, the directrix is parallel to xaxis, the standard equation of a parabole becomes, x2 = 4ay




Vertical Shifts Of Quadratic Functions Ck 12 Foundation




Plot A Graph For The Equation Y X 2 4x 1
Examples (y2)=3(x5)^2 foci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=x^{2}A particle moves along the parabola {eq}y = x^2 {/eq} in the first quadrant in such a way that its {eq}x {/eq}coordinate (measured in meters) increases at a steady {eq}\rm 10\ m/sec {/eq}👉 Learn how to graph quadratic equations in vertex form A quadratic equation is an equation of the form y = ax^2 bx c, where a, b and c are constants



Graphing Quadratic Functions



Quadratic Function Parabola
Graph the parabola, y =x^21 by finding the turning point and using a table to find values for x and yIn the figure, the vertex of the graph of y=x 2 is (0,0) and the line of symmetry is x = 0 Definition Parabola 1Algebric A Parabola is the graph of a quadratic relation of either form where a ≠ 0;Please be sure to answer the questionProvide details and share your research!




Content Transformations Of The Parabola
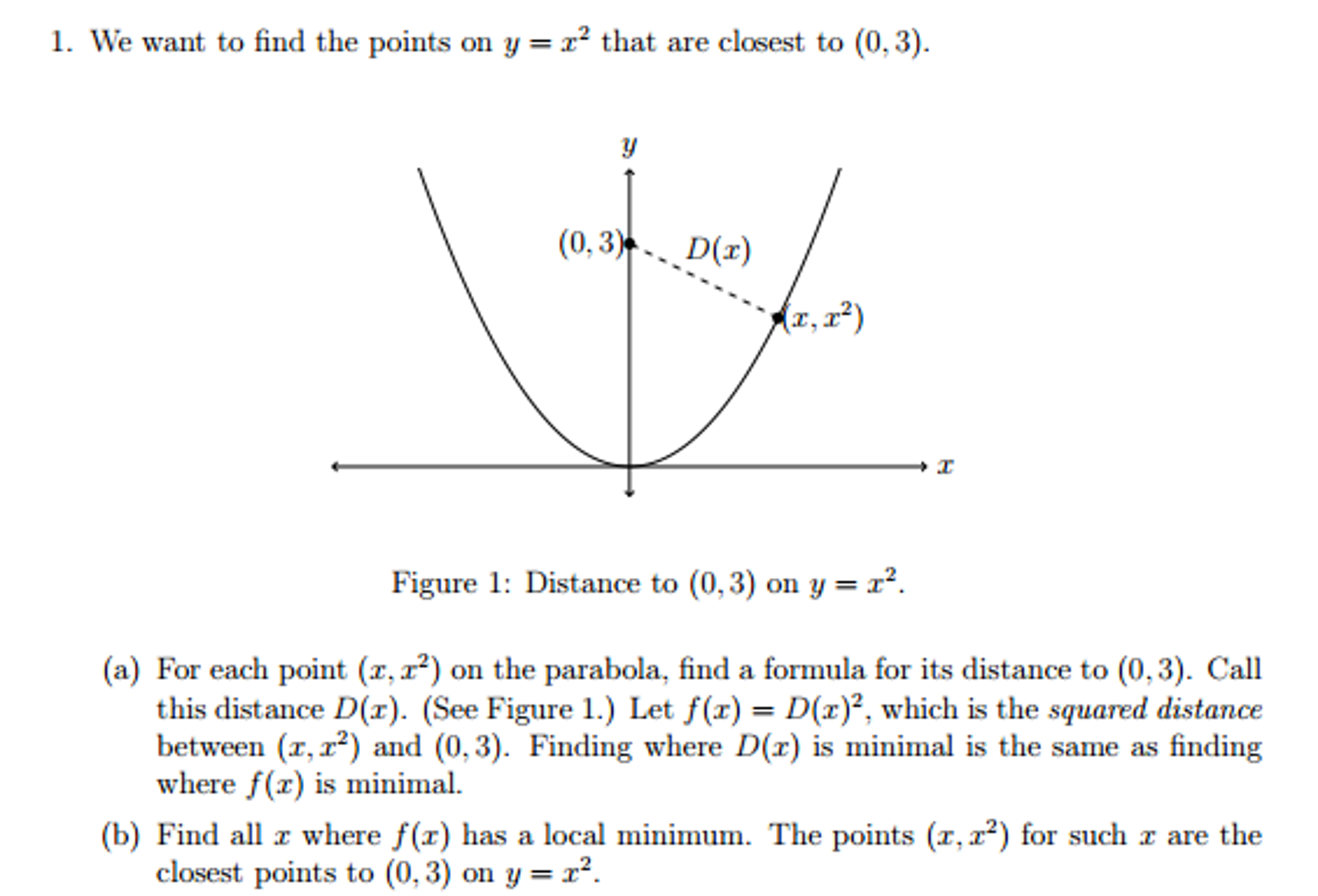



We Want To Find The Points On Y X 2 That Are Chegg Com
I do not know how to graph the parabola y= x^2 Plot a few points and draw a smooth curve thru themWhen graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if aGraph y=(x2)^24 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola opens up or down




How To Graph A Parabola With No X Intercepts Y X 2 2 Youtube



How To Graph Y X 2 1 Youtube
Y = ax 2 bx c or x = ay 2 by c 2 Geometric A parabola is This should do import matplotlibpyplot as plt import numpy as np # create 1000 equally spaced points between 10 and 10 x = nplinspace (10, 10, 1000) # calculate the y value for each element of the x vector y = x**2 2*x 2 fig, ax = pltsubplots () axplot (x, y) This is your approach with as few changes as possible to make it workThe vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, and the vertex is (0, 3) Observe the graph of y



How Do I Graph The Quadratic Equation Y X 1 2 By Plotting Points Socratic



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2
And y = −√ x (the bottom half of the parabola) Here is the curve y 2 = x It passes through (0, 0) and also (4,2) and (4,−2) Notice that we get 2 values of y for each value of x larger than 0 This is not a function, it is called a relationThe equation of the common tangent touching the circle (x − 3) 2 y 2 = 9 and the parabola y 2 = 4 x above the xaxis is View solution Two straight lines are perpendicular to each other, one of them touches the parabola y 2 = 4 a ( x a ) and the other touches y 2 = 4 b ( x b )Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e − ( x 1 2) 2 9 4 ( x 1 2) 2 9 4 − ( x 1 2) 2 9 4 ( x 1 2) 2 9 4 Set y y equal to the new right side y = − ( x 1 2) 2 9 4 y = ( x 1 2) 2 9 4




How To Graph Y X 2 1 Youtube



Graphing Quadratic Functions
Using integration find the area of region bounded by the triangle whose vertices are (1, 0), (2, 2) and (3, 1) View solution Find the area of the region bounded by the parabola y = x 2 and y = ∣ x ∣Graph a function by translating the parent functionWe're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2 , where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0




Graph Y X 2 3 Youtube



Quadratics Graphing Parabolas Sparknotes
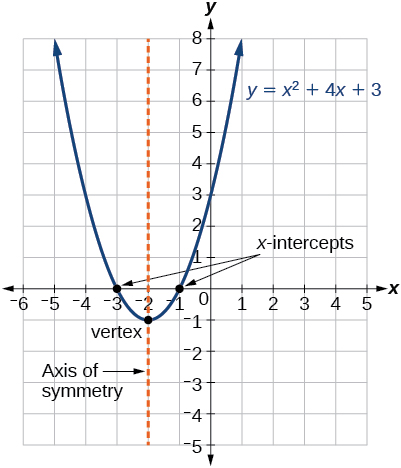
Question I do not know how to graph the parabola y= x^2 Found 2 solutions by stanbon, jim_thompson5910 Answer by stanbon(757) (Show Source) You can put this solution on YOUR website!What is the following parabola's axis of symmetry of $$ y =x^2 2x 3 $$ Answer Since this equation is in standard form, use the formula for standard form equation $$ x = \frac{ b}{ 2a} $$ Answer the axis of symmetry is the line $$ x = 1 $$ Problem 7 What is the following parabolaThe x coordinate of the vertex is the equation of the axis of symmetry of the parabola The vertex of the parabola is (2, 1) So, the axis of symmetry is the line x = 2 Find the axis of symmetry of the graph of y = x2 − 6x 5 using the formula For a quadratic function in standard form, y = ax2 bx c , the axis of symmetry is a



Exploration Of Parabolas
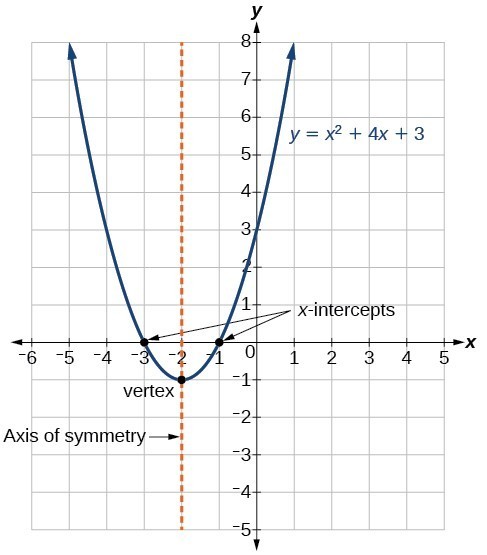



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
Y = ( x 3 2) 2 − 17 4 y = ( x 3 2) 2 17 4 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 1 a = 1 h = − 3 2 h = 3 2 k = − 17 4 k = 17 4 Since the value of a a is positive, the parabola opens up Opens Up Find the vertex ( h, k) ( h, k) The #x^2# is positive so the general graph shape is #uu# Consider the generalised form of #y=ax^2bxc# The #bx# part of the equation shifts the graph left or right You do not have any #bx# type of value in your equation So the graph is central about the yaxis The #c# part of the equation is of value 1 so it lifts the vertex up from y=0 to y=1Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with 1 1 in the expression f ( 1) = − ( 1) 2 5 ( 1) − 2 f ( 1) = ( 1) 2 5 ( 1) 2 Simplify the result
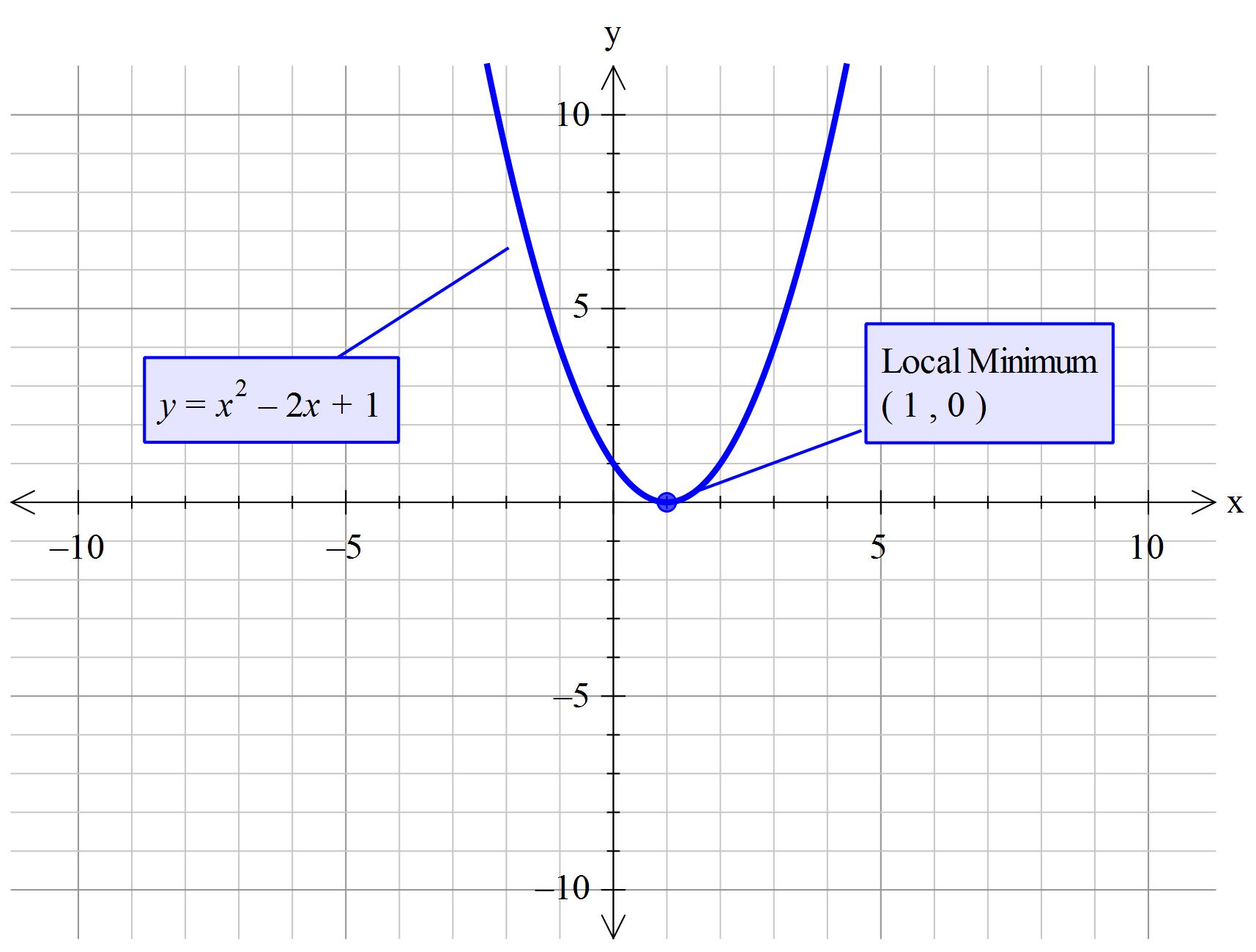



What Is The Vertex Of Y X 2 2x 1 Socratic




5 Write The Equation Of The Parabola In Vertex Form Chegg Com
The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetryY = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, y See below y=x^24 Since y has no term in x we know that the axis of symmetry of it's parabolic graph is the line x=0 y(0) = 4 > y_"vertex" = (0,4) We also know that y_"vertex" will be an absolute extremum of y Since x^2>=0 forall x in RR > y_"vertex" = y_"min" Finally, we need to find the zeros of y x4=0 > x=2 y has x intercepts at (2,0) and (2,0) Using this




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy




Solution For The Parabola Y X 2 36 Graph Of A Parabola Opening Down At The Vertex 0 36 Crossing The X Axis At 6 0 And 6 0
Just complete square the stuff and the result will pop up y = 1( x^2 6x 5) = 1 x^2 2x(3) 3^2 3^2 5 y = 1(x3)^2 14 = 1( x (3) ) 14 So the vertex ( 3 , 14) In y = x^2 we're done, that is the y value In y = (x2)^2, after we square, we are done, that is the y value In y = (x2)^2 3, after we square, we still need to subtract 3 from the number, that moves us down 3 The vertex of y=x^2 is the point (0,0) The vertex of y = (x2)^23 is the point (2,3)Parabolas A quadratic function is a function that can be written in the form f ( x) = a x 2 b x c where a, b, and c are real numbers and a ≠ 0 This form is called the standard form of a quadratic function The graph of the quadratic function is a Ushaped curve is called a parabola The graph of the equation y = x 2, shown below, is a



Practice Exam 1



Graphing Quadratic Functions
Column 1 (a) The set of real values of a for which two distinct tangents can be drawn from (a 3, a) to the parabola y2 = 4x (b) The set of real values of a for which at least one tangent to the parabola y2 = 4ax is normal to the circle x2 y2 − 2ax − 4ay − a2 = 0 (c) A set of values of a for which a is the distance between parallelSelect a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with 6 6 in the expression f ( 6) = ( 6) 2 − 14 ⋅ 6 48 f ( 6) = ( 6) 2 14 ⋅ 6 48 Simplify the result Thanks for contributing an answer to Mathematics Stack Exchange!



Solution Graph The Parabola Y X 4 2 2




Graph Y X 2 Study Com
Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis You don't say what the goal of this problem is, which leaves others guessing I'd venture that you want to know how the function y=x^2 changes if the graph (parabola) is shifted up by 4 units This is vertical translation The new function will be g (x) = x^2 4 kvargli6h and 41 more users found this answer helpful heart outlined A Quadratic Equation takes the form y = ax2 bx c Graph of a quadratic function forms a Parabola The coefficient of the x2 term (a) makes the parabola wider or narrow If the coefficient of the x2, term (a) is negative then the parabola opens down
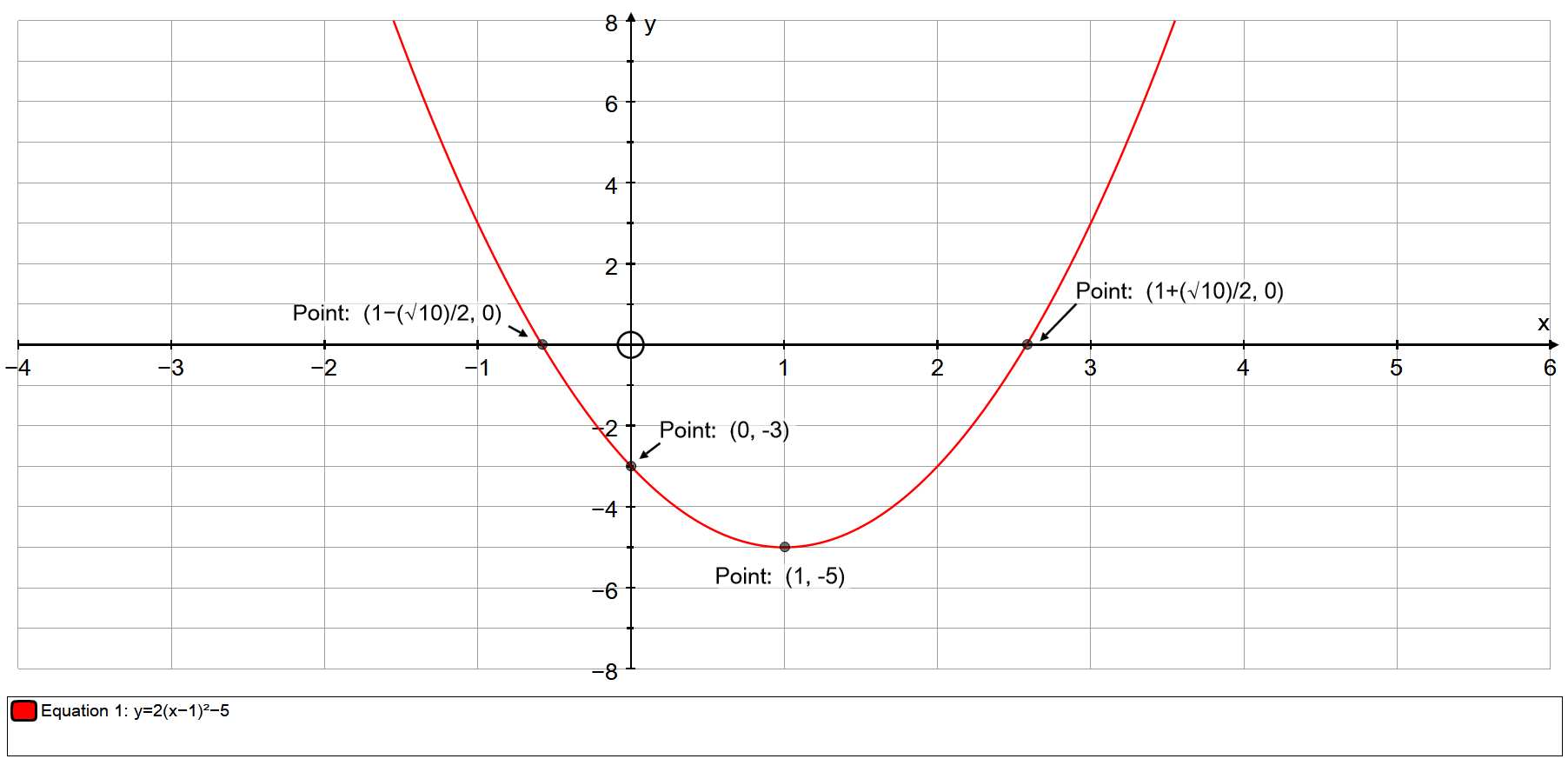



How Do You Graph The Parabola Y 2 X 1 2 5 Using Vertex Intercepts And Additional Points Socratic




Content Transformations Of The Parabola



Instructional Unit The Parabola Day 4 And 5




Three Tangent Lines To The Parabola Y X 2 Corresponding To Three 1d Download Scientific Diagram




Using Properties Of Parabolas To Graph A Parabola Algebra And Geometry Help




How To Draw Y 2 X 2
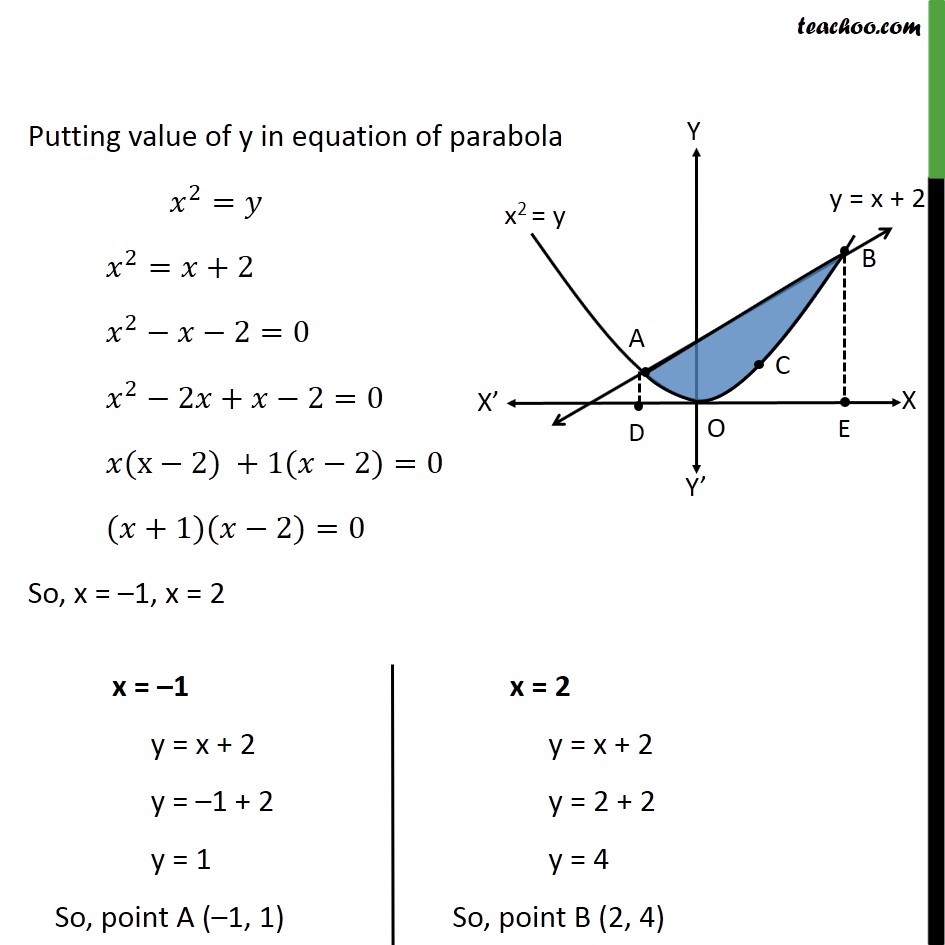



Misc 10 Find Area Enclosed By Parabola X2 Y T X 2
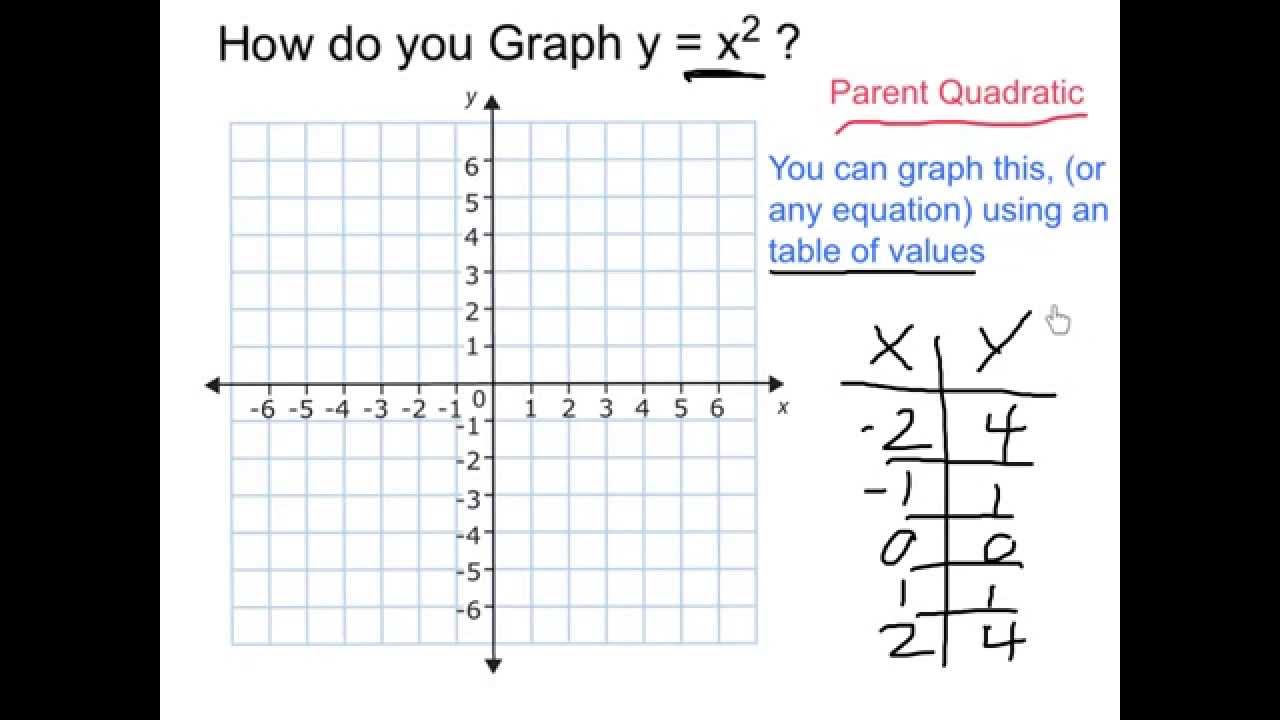



Graph Y X 2 Youtube
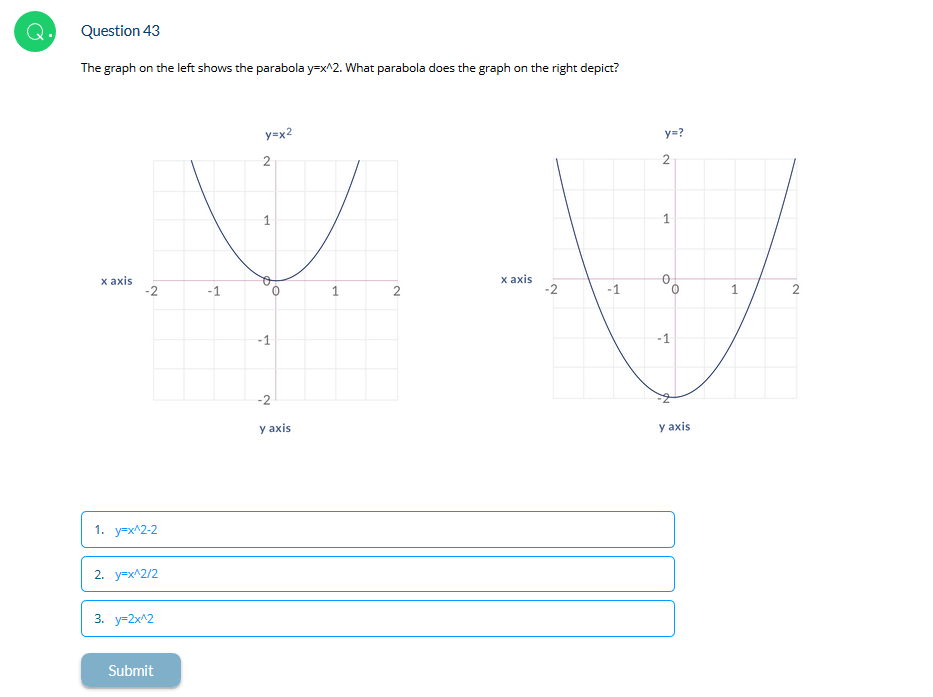



Question 43 The Graph On The Left Shows The Parabola Chegg Com




Quadratic Function
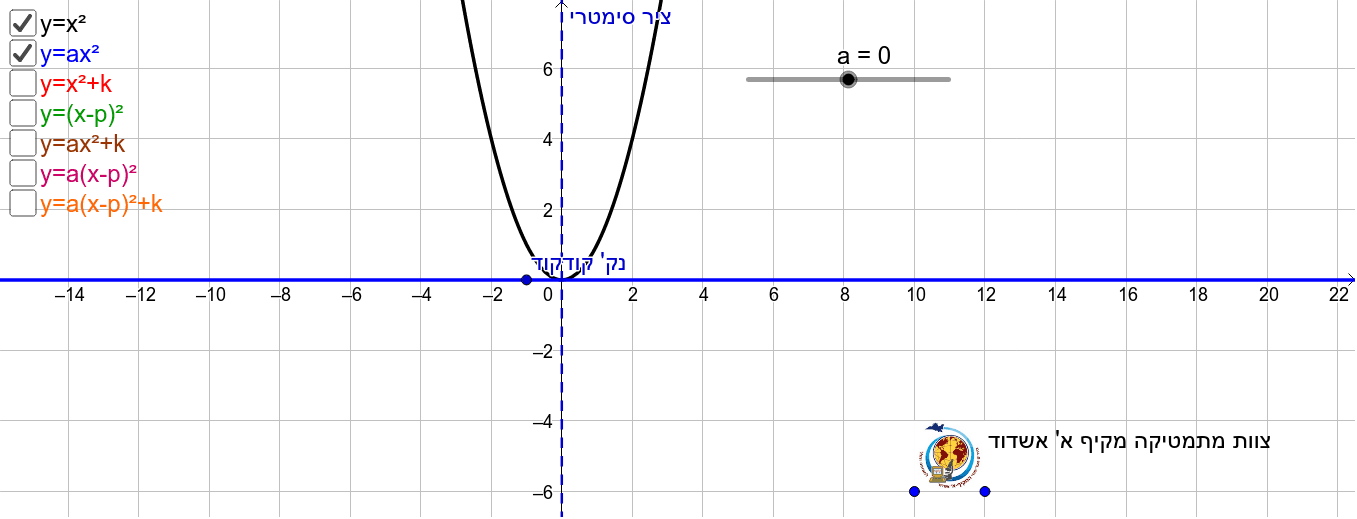



Parabola Y X 2 Geogebra



How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic
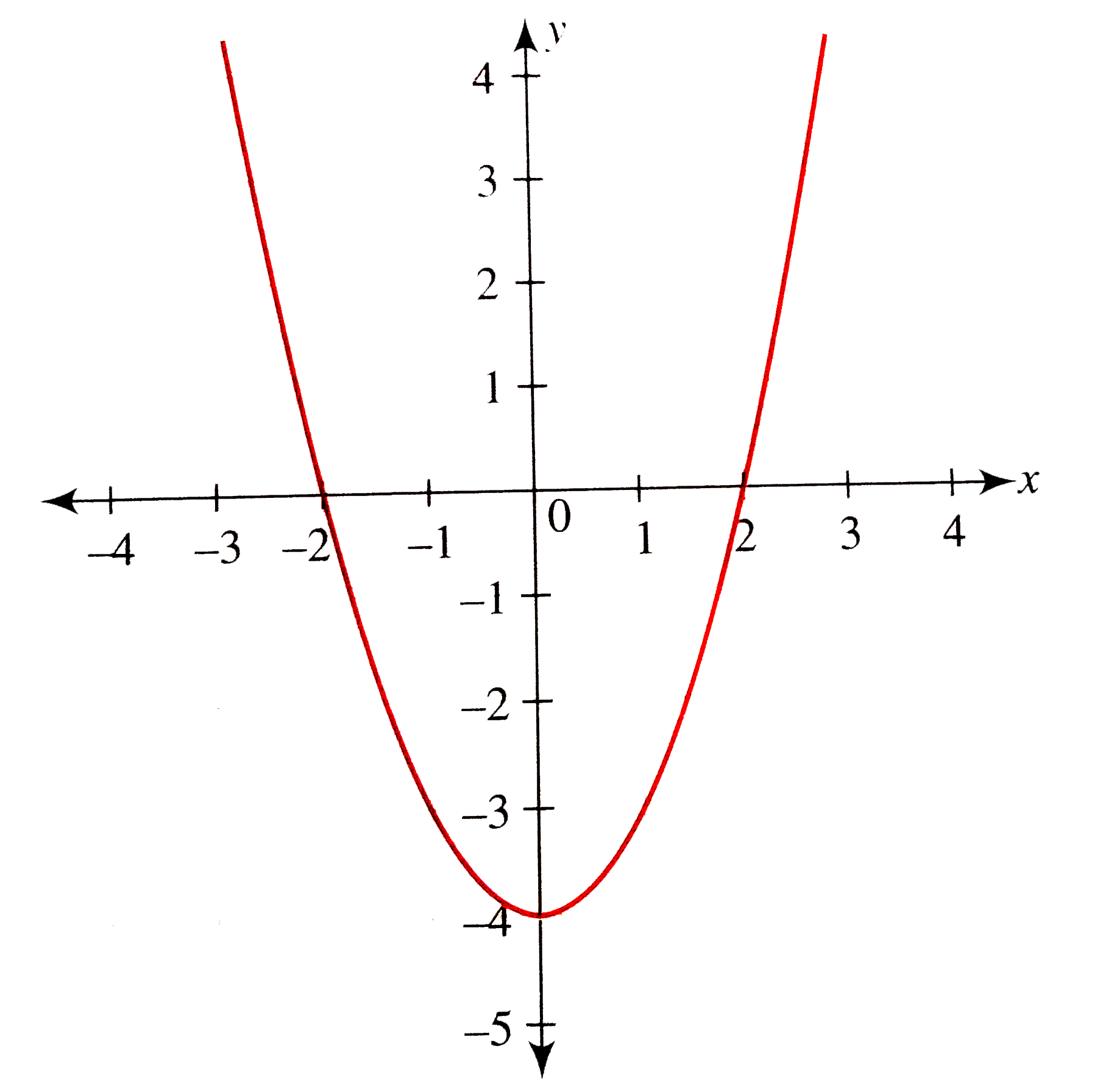



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4



5 2 Quadratic Functions Mathematics Libretexts



Parabolas




How To Draw Y 2 X 2




The Graph Of The Quadratic Function Y X2 Is Shown Below If This Parabola Is Reflected About The Brainly Com




Consider The Parabola Y X 2 The Shaded Area Is Brainly In



1




Quadratic Function
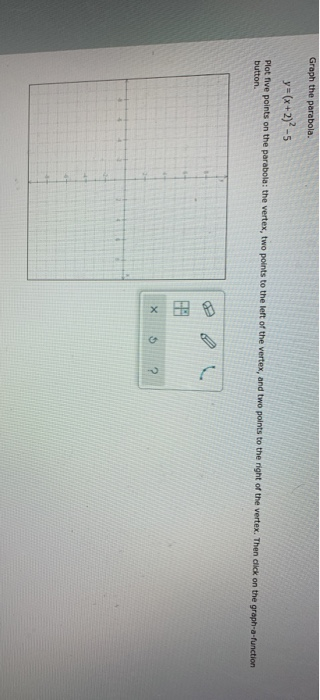



Graph The Parabola Y X 2 2 5 Plot Five Points On Chegg Com



Graph The Parabola Y X 2 6x Mathskey Com
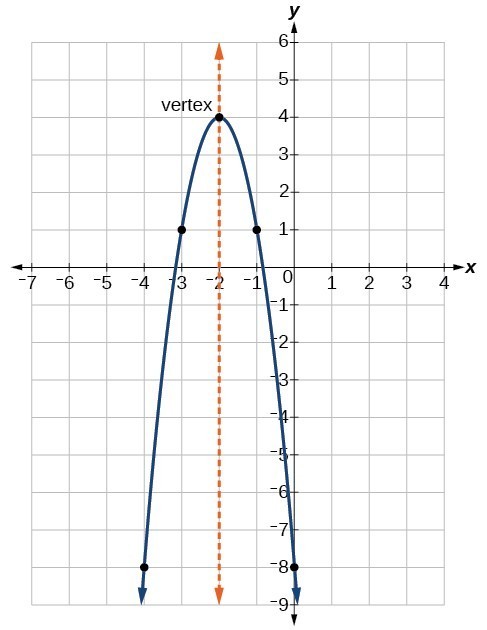



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Graphing Quadratic Functions Lesson Article Khan Academy
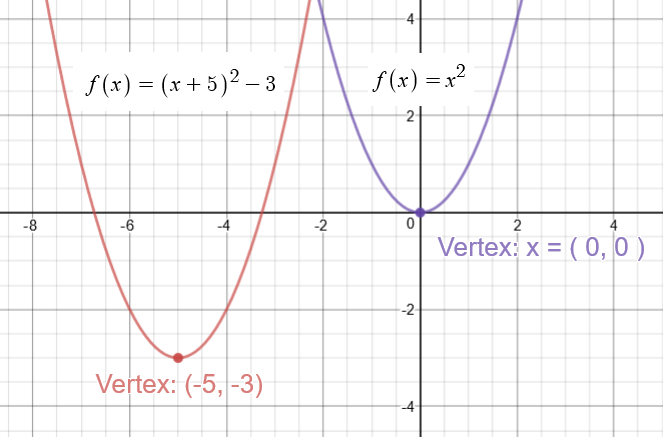



How To Graph A Parabola Y X 5 2 3 Socratic




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic



Math Spoken Here Classes Quadratic Equations 3




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com



Quadratics Graphing Parabolas Sparknotes
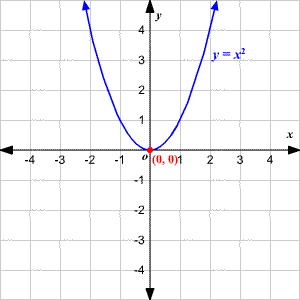



Parabolas



1
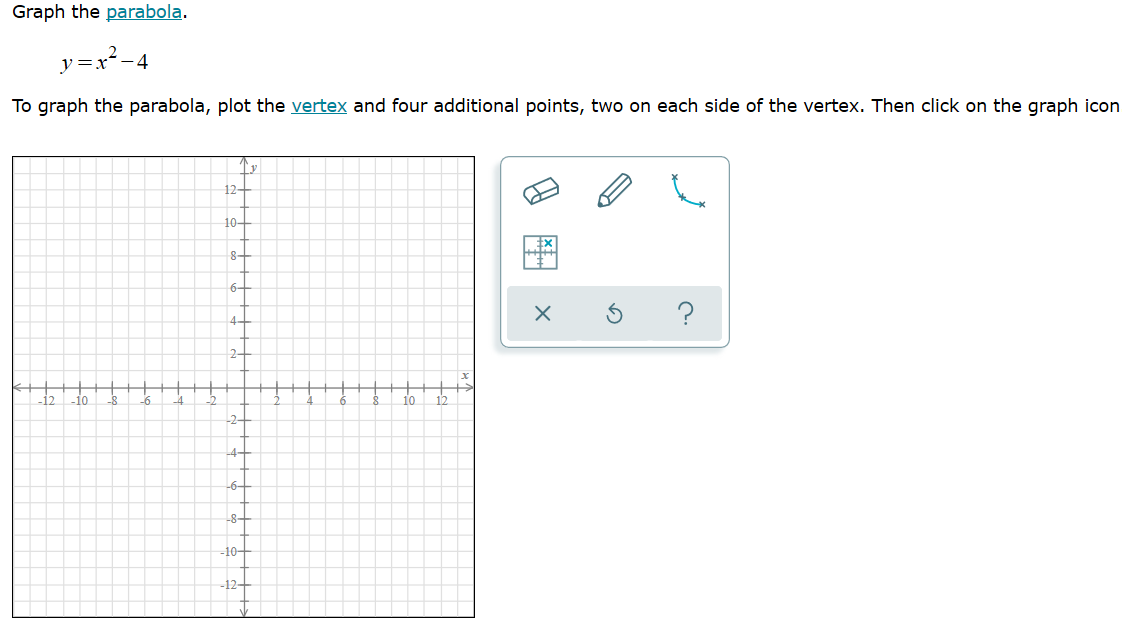



Graph The Parabola Y X2 4 To Graph The Parabola Chegg Com




The Distance Between The Vertex Of The Parabola Y X 2 4x




How To Draw Y 2 X 2
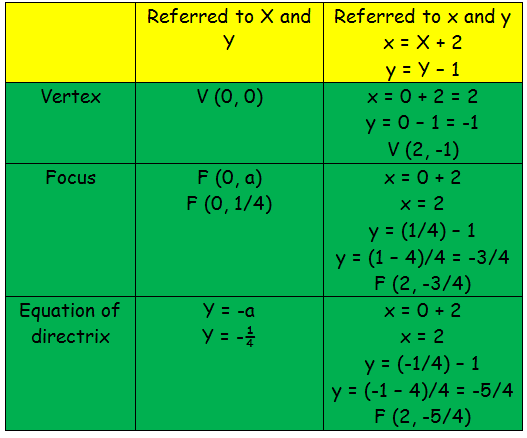



How To Find Focus Directrix And Vertex Of Parabola
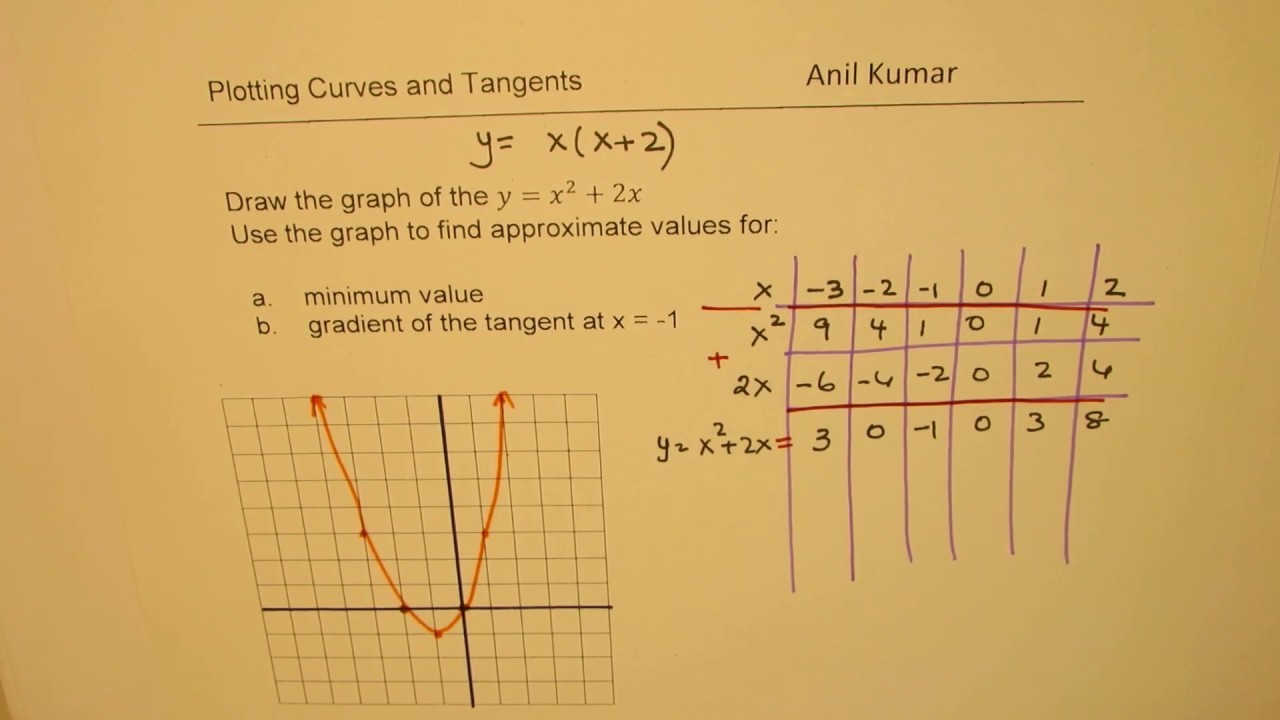



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
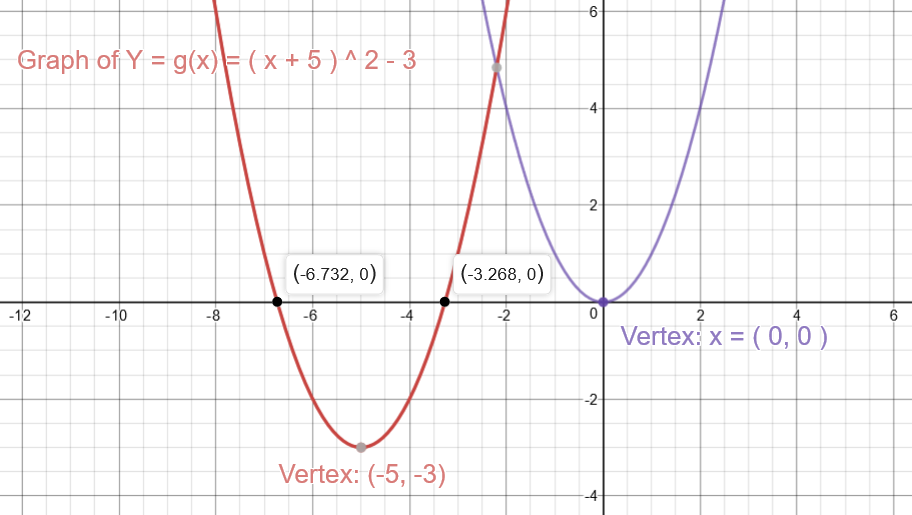



How To Graph A Parabola Y X 5 2 3 Socratic



Math Spoken Here Classes Quadratic Equations 3
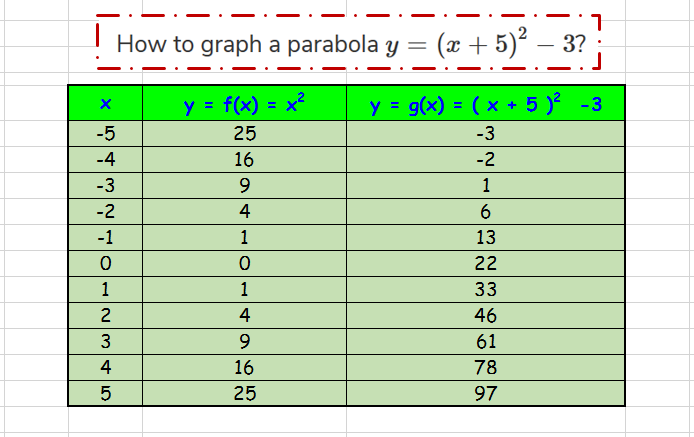



How To Graph A Parabola Y X 5 2 3 Socratic



How To Draw A Sketch Of The Graph Of The Parabola Y X 2 8x 10 Quora
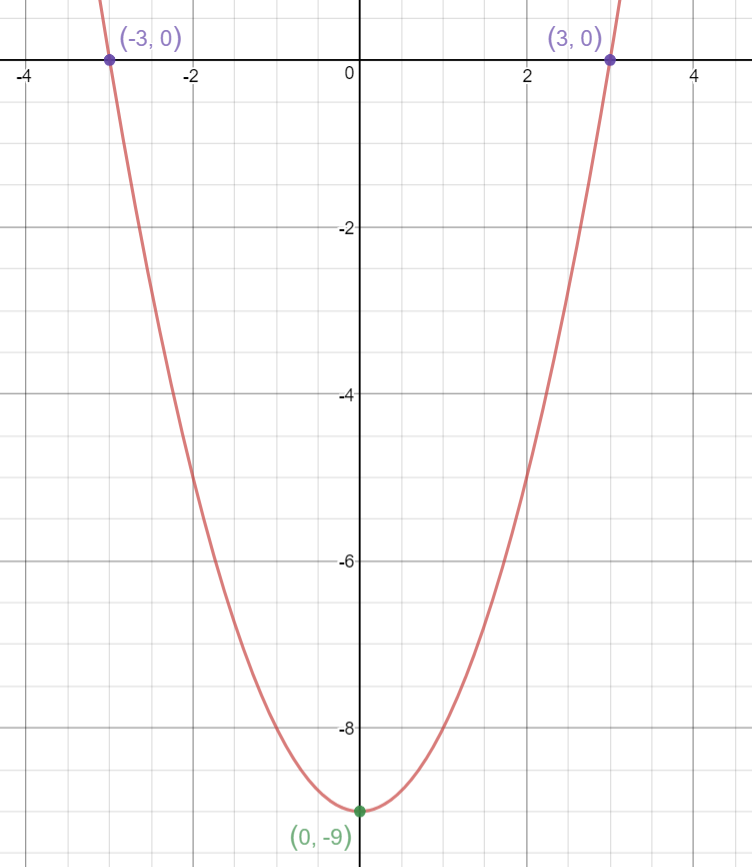



How Do You Graph Y X 2 9 Socratic



Instructional Unit The Parabola Day 4 And 5



Solution I Do Not Know How To Graph The Parabola Y X 2
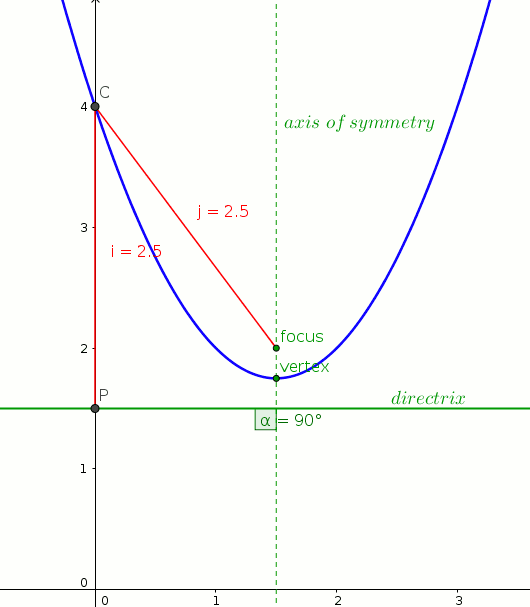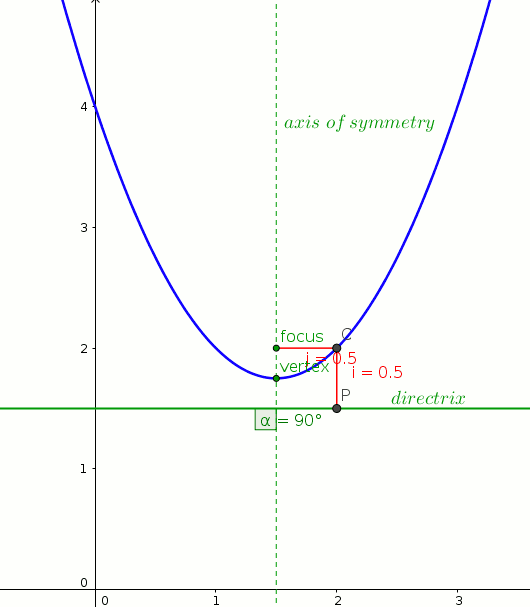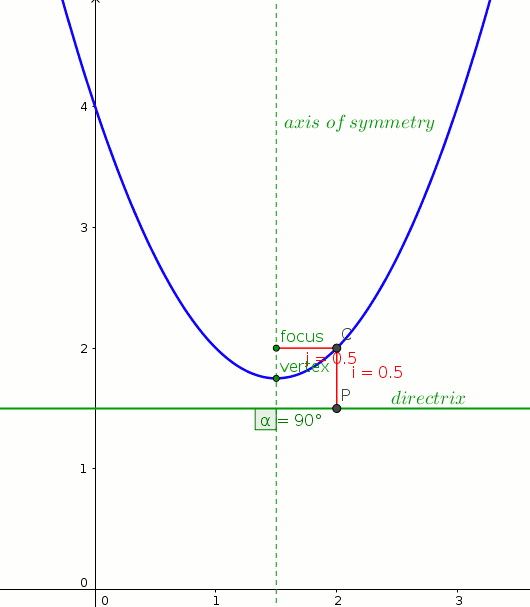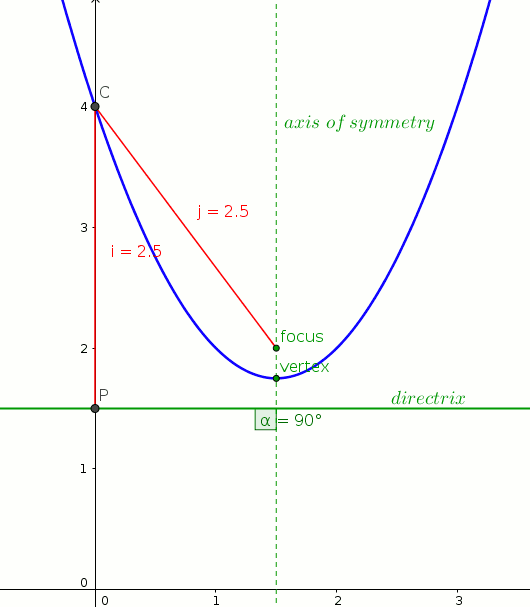



What Are The Vertex Focus And Directrix Of Y X 2 3x 4 Socratic
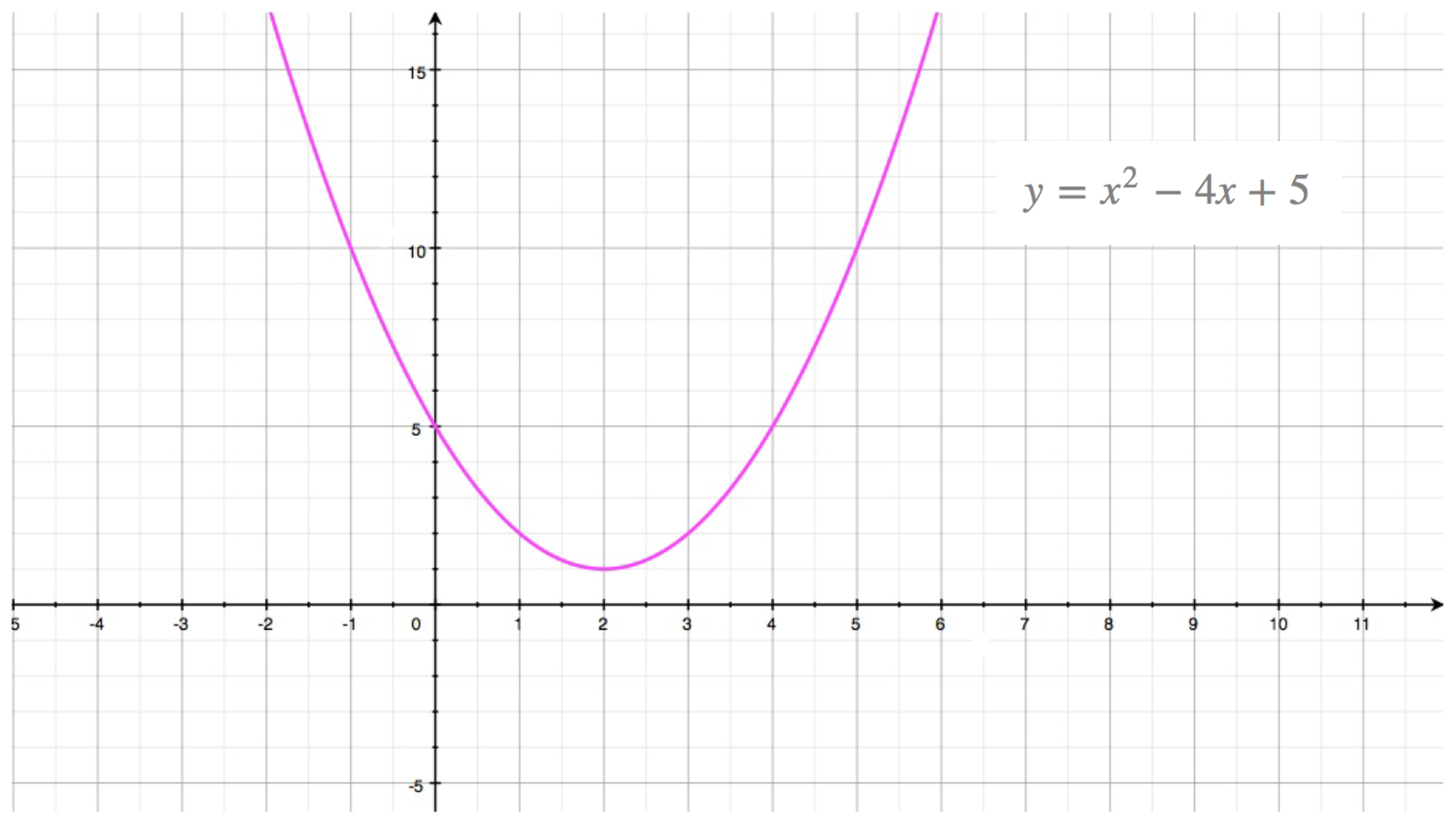



Quadratic Function Parabola
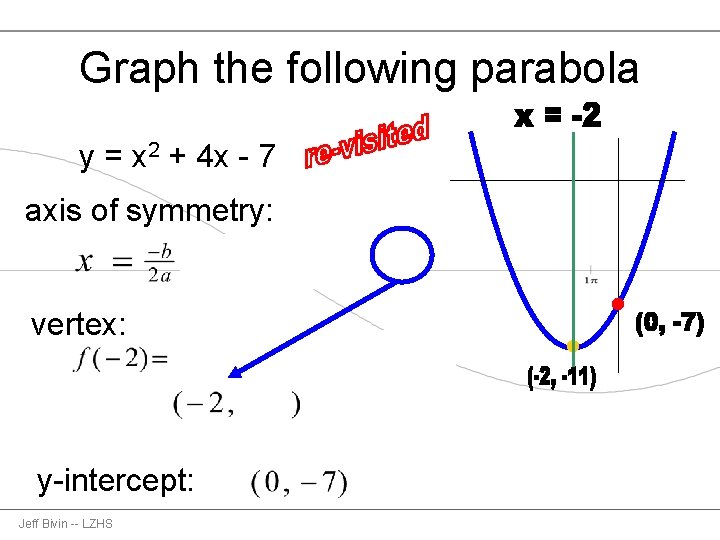



Graphing Parabolas Using The Vertex Axis Of Symmetry



Quadratics Graphing Parabolas Sparknotes




Quadratic Function




The Graph Below Is A Parabola So It Can Be Represented By A Quadratic Function Which Of The Brainly Com
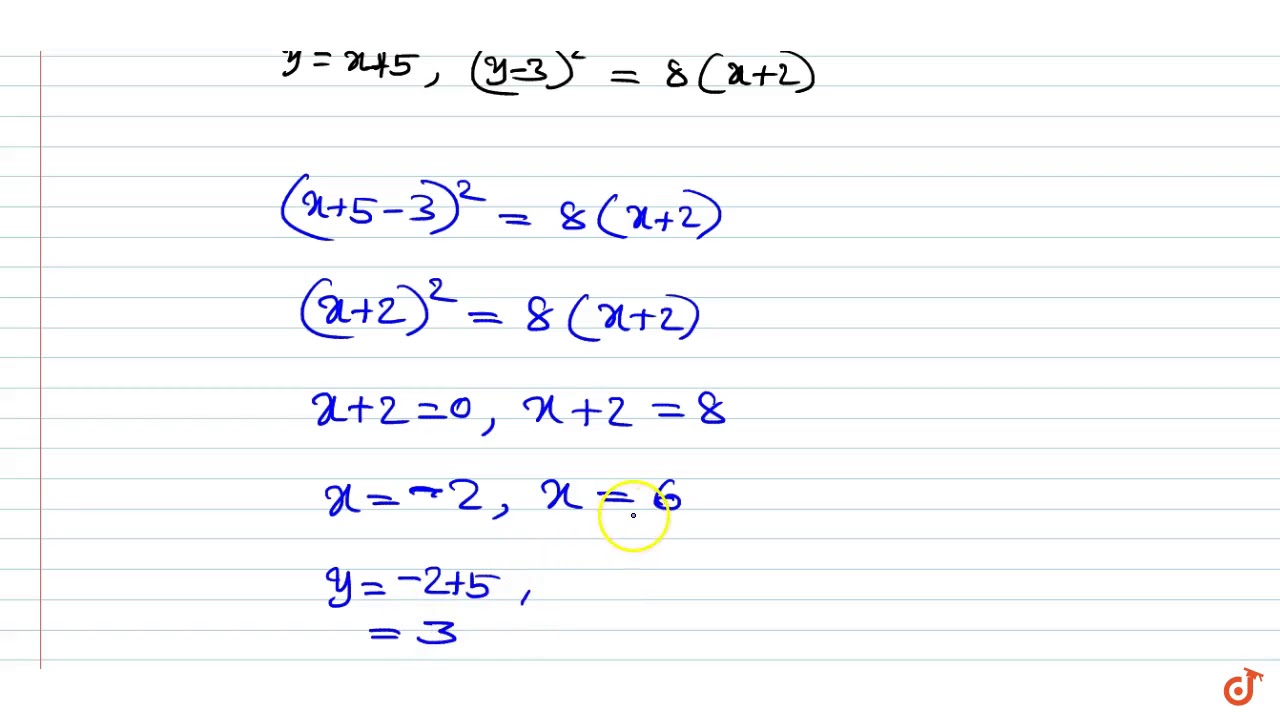



A Line Y X 5 Intersect The Parabola Y 3 2 8 X 2 At A B Find The Length Of Chord Ab Youtube




Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Graphing Parabolas



Solution How To Graph A Parabola Using Y X2 2x 8
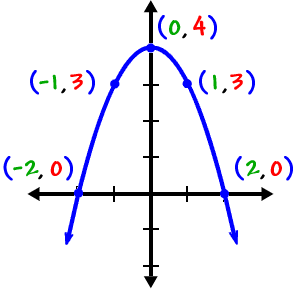



Graphing Quadratics Parabolas Cool Math Algebra Help Lessons Graphing Parabolas Overview



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively



Math Spoken Here Classes Quadratic Equations 3




Image Of A Parabola Whose Equation In The Object Plane Is Y X 2 And Image Of Parabola Whose Equation Is Y 1 X 2 Mathematics Stack Exchange
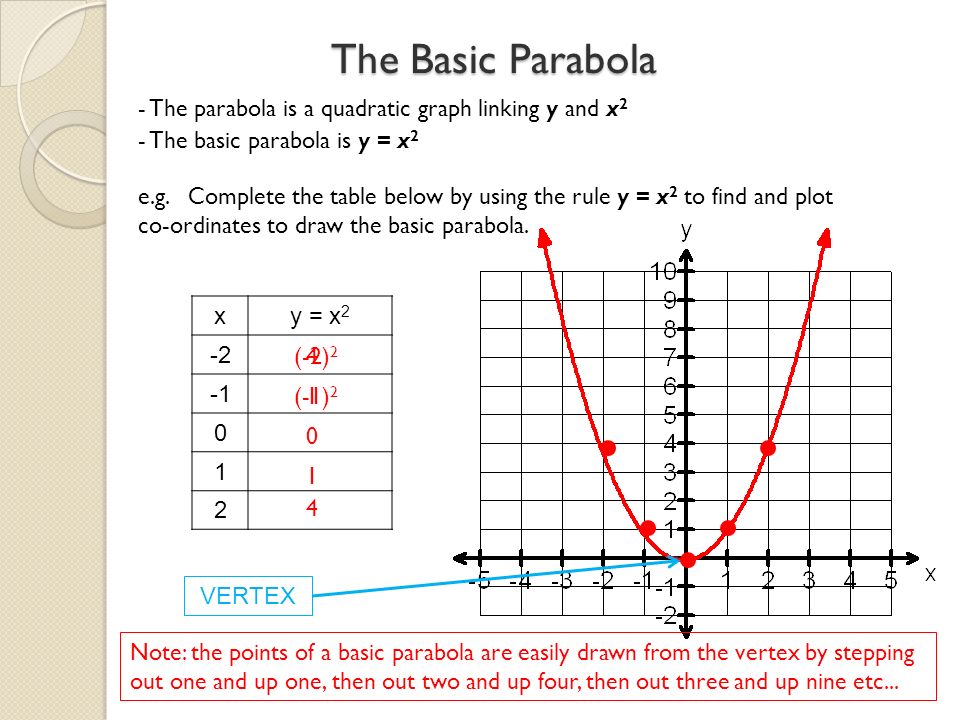



Parabolas Ppt Download
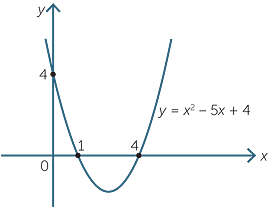



Quadratic Function




Find The Area Of The Region Bounded By The Parabola Y X 2 And The Line Y 4 Study Com



Sketch The Parabola Of Equation Y X 2 6x 9 And Indicate Its Vertex Study Com
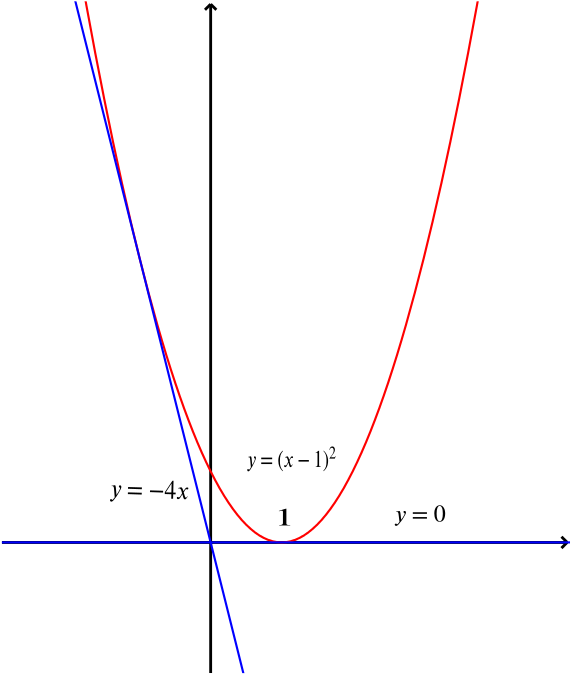



Solution When Does Y Kx Intersect The Parabola Y X 1 2 Quadratics Underground Mathematics




Scaling Reflecting Parabolas Video Khan Academy



Y X 2
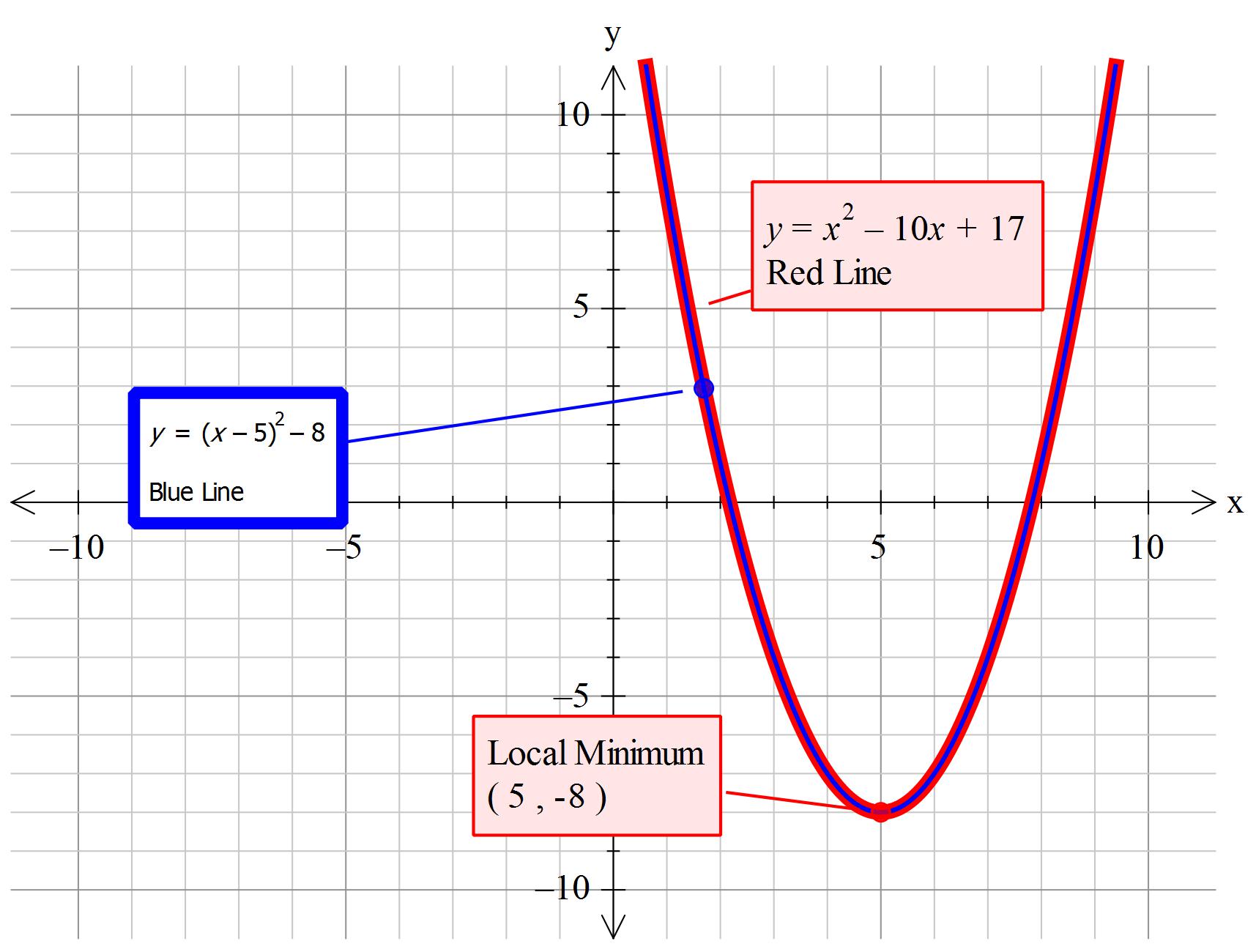



How Do You Write The Vertex Form Equation Of The Parabola Y X 2 10x 17 Socratic



Y X 2 2



Solution Graph Y X 2 1 Label The Vertex And The Axis Of Symmetry And Tell Whether The Parabola Opens Upward Or Downward
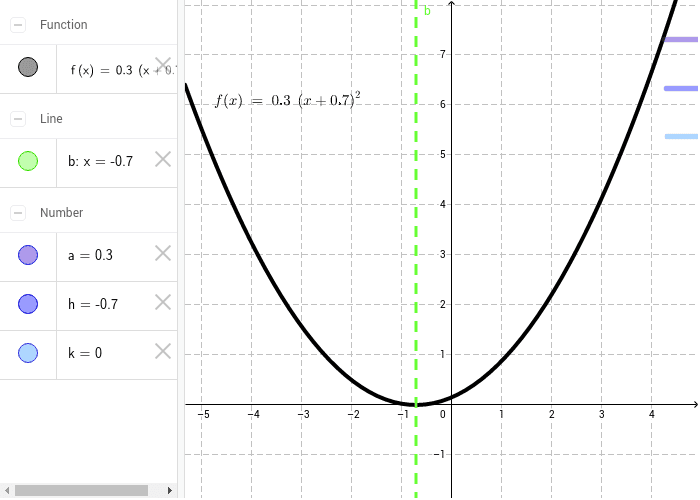



Transformations To The Graph Of Y X 2 Geogebra




Content Transformations Of The Parabola



Math Spoken Here Classes Quadratic Equations 3
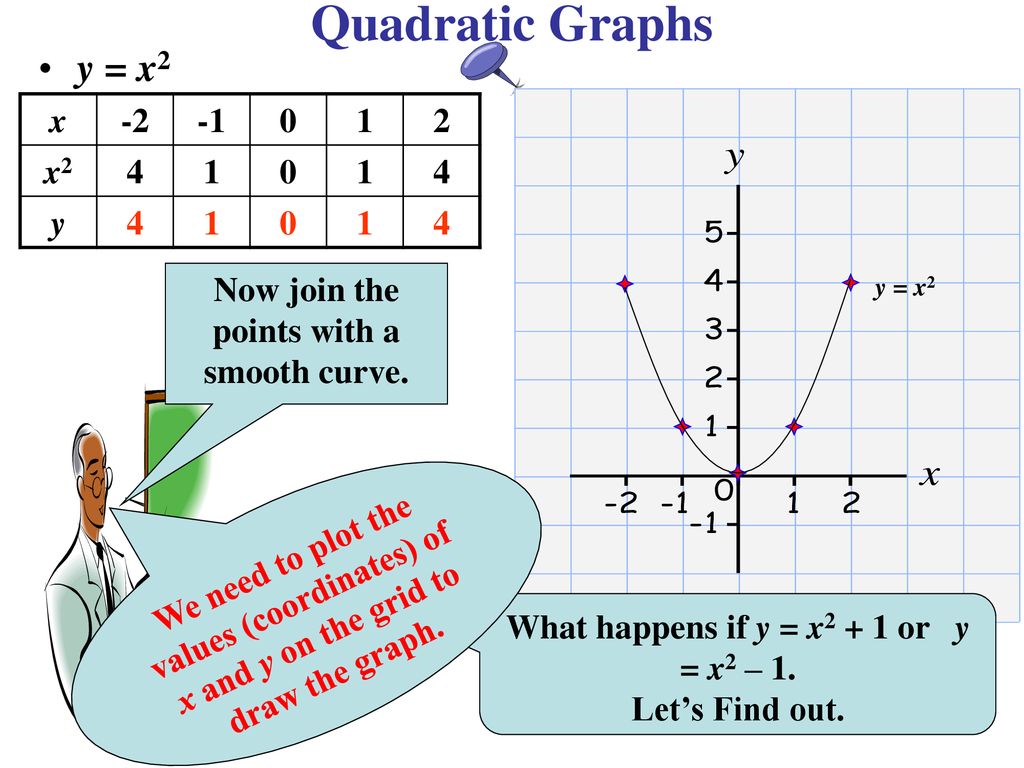



Quadratic Graphs Parabolas Ppt Download
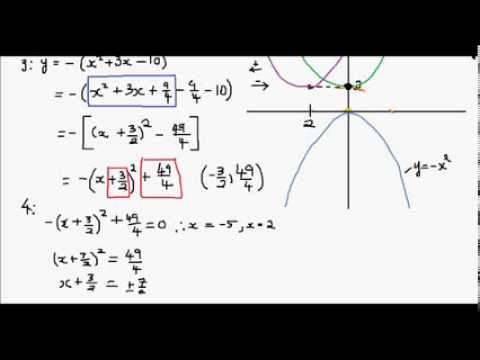



How To Sketch A Parabola Example 1 Y X 2 3x 5 Youtube
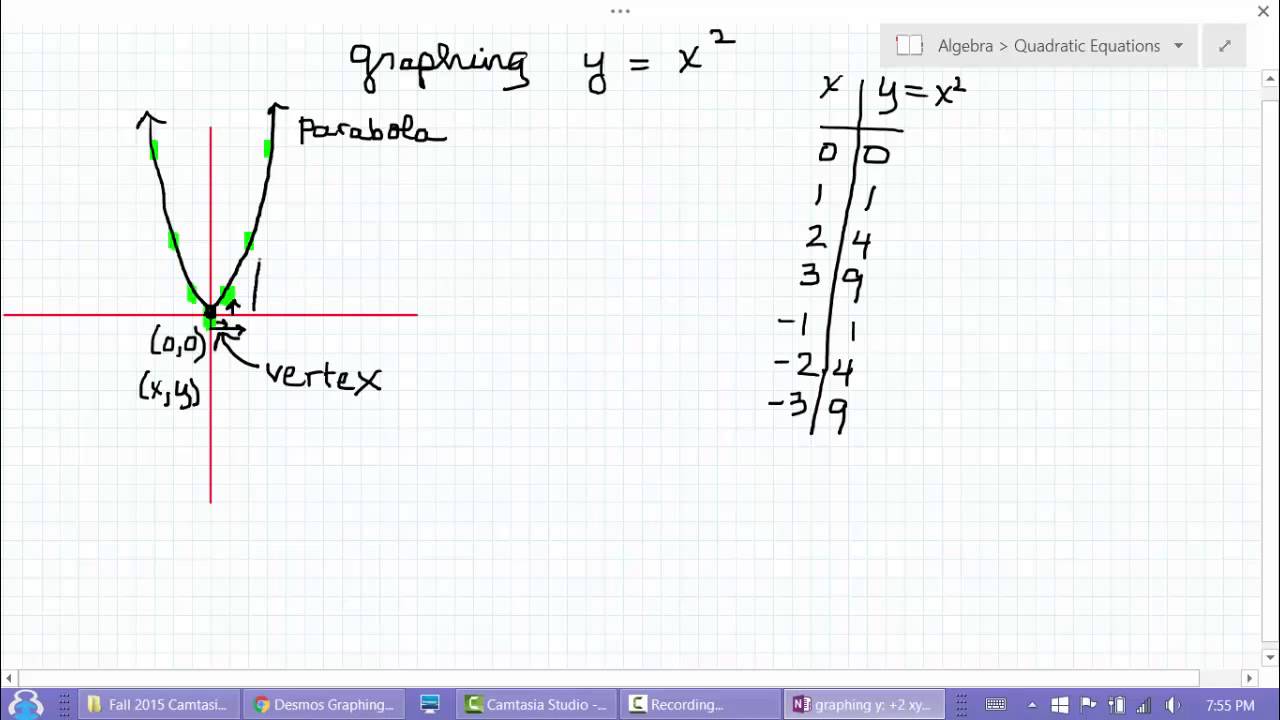



Graphing Simple Non Linear Relationships 9 Alamandamaths



Why Does The Line Of Symetry Of A Parabola Occurs When Math X Frac B 2a Math Quora
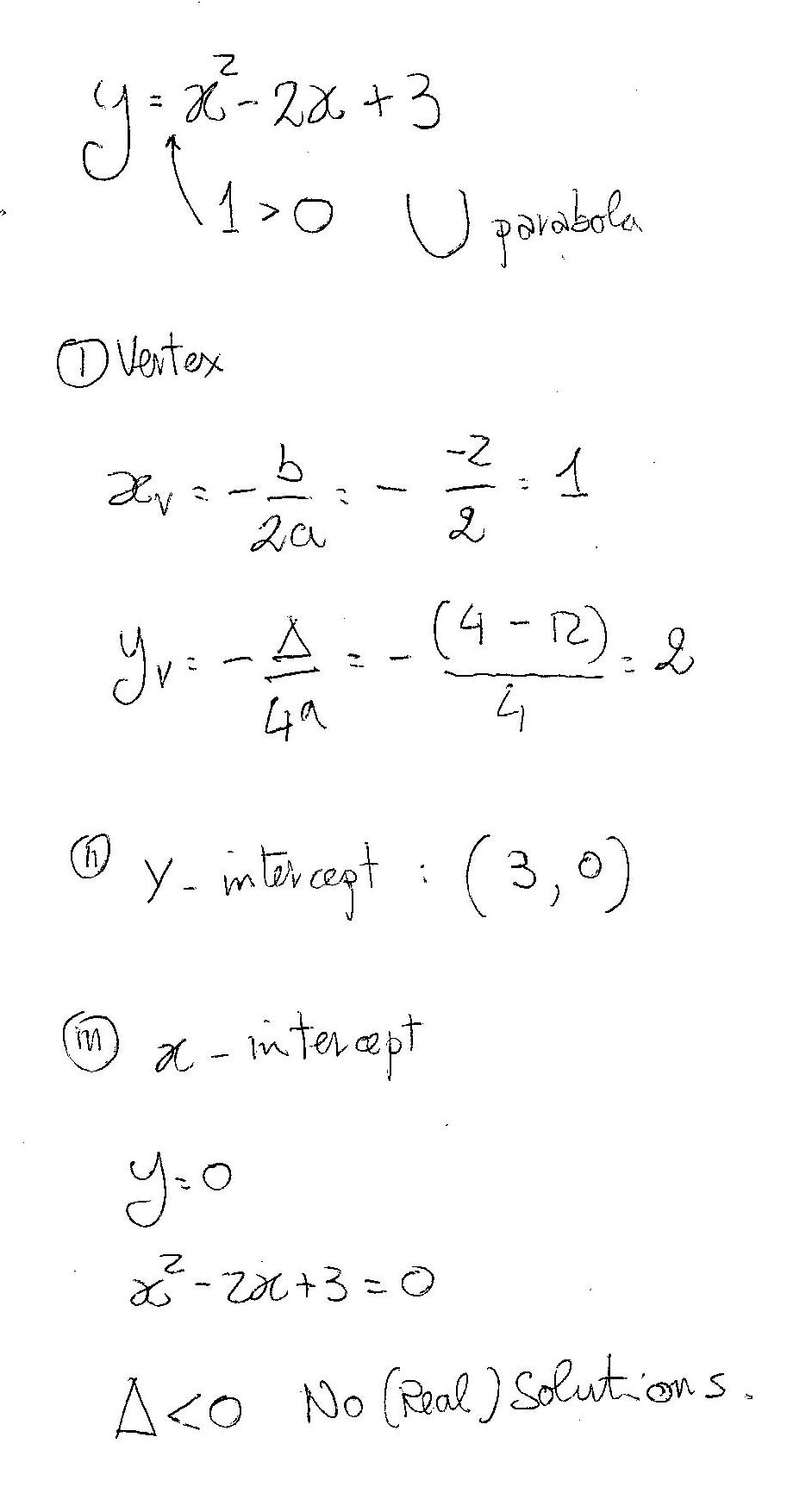



How Do You Graph Y X 2 2x 3 Socratic



Search Q Y 3d1 X Tbm Isch



Quadratics Graphing Parabolas Sparknotes



コメント
コメントを投稿